한눈에 빈도 분포를 파악하는 히스토그램에 관한 모든 것

현실적으로 방대한 양의 데이터를 살펴보는 건 쉽지 않기 때문에, 한눈에 데이터를 이해할 수 있도록 그래프로 정리하여 데이터 시각화해야 합니다. 이번 포스트에서는 자료의 빈도 분포를 한눈에 파악할 수 있는 히스토그램에 관해 자세히 알아보겠습니다. 히스토그램은 단순 막대그래프와 생김새는 유사하지만, 차이점이 확실하니 유념하셔야 합니다.

Part1: 히스토그램에 관해 알아보기

1.히스토그램이란

히스토그램은 방대한 양의 데이터를 구분하여 빈도를 파악하는 도수분포표를 그래프로 시각화한 것입니다. 도수분포표는 측정값이 존재하는 범위를 계급으로 나누고 각 계급의 도수를 조사하여 나타낸 표이며, 이때 변량을 일정한 간격을 나눈 구간을 계급, 각 계급에 속하는 자료의 수를 도수라고 합니다. 히스토그램은 도수분포표의 각 계급의 양 끝값을 가로축에 표시하고 그 계급의 도수를 세로축에 표시하여 막대그래프로 표현합니다. 

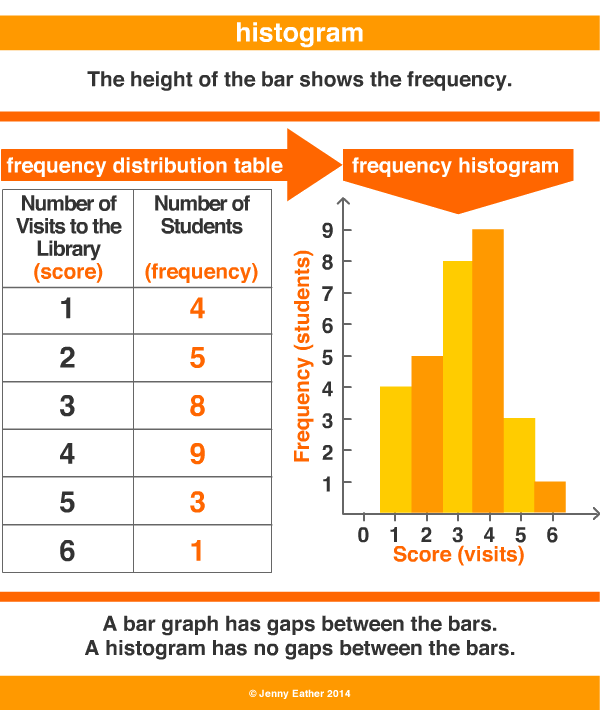
출처: http://www.amathsdictionaryforkids.com/

2. 히스토그램 특징

• 히스토그램을 통해 자료의 분포 상태를 한눈에 알아볼 수 있습니다.
• 히스토그램의 직사각형 가로 길이는 일정하므로 직사각형 세로 길이인 넓이는 각 계급의 도수에 정비례합니다.
  (직사각형의 넓이) = (각 계급의 크기) × (그 계급의 도수)
• (직사각형의 넓이의 합) = {(각 계급의 크기) × (그 계급의 도수)}의 총합 = (계급의 크기) × (도수의 총합)

3. 히스토그램 역사

히스토그램이란 개념은 1895년 영국 통계학자 칼 피어슨(Karl Pearson)에 의해 처음 소개되었습니다. 칼 피어슨은 데이터 분포를 시각화하는 방법을 찾는 데에 관심이 있었고 이를 위한 도구로 히스토그램을 개발했습니다. 그는 데이터 분포를 시각화하고 다양한 변수 간의 관계를 연구하고 데이터 분포의 패턴을 식별하기 위해 히스토그램을 사용했고,  연구자들과 분석가들 사이에서 히스토그램은 빠르게 데이터 분석하는 도구로 인정받았습니다. 공학, 생물학 및 사회 과학을 포함한 다양한 분야에서 사용이 확대되었고 오늘날 히스토그램은 데이터 시각화에 계속 널리 사용되며 데이터 분석 도구 및 소프트웨어 패키지에서 중요하게 사용됩니다.

출처: https://wellcomecollection.org/

4. 히스토그램 어원

히스토그램(Histogram)에서 ‘히스토(Histo)’의 어원에 관해 두 가지 설이 있습니다. 첫 번째는 그리스어에서 똑바로 선 것(Anything upright)를 뜻하는 ‘히스토스(Histos)’에서 유래했다는 점입니다. 즉 히스토그램에는 똑바로 선 세로 막대가 있다는 것을 의미합니다. 두 번째는 역사를 의미하는 ‘히스토리(History)’를 줄인 것으로 추측됩니다. 즉 히스토그램은 통계적인 분포를 그림으로 표현한 역사라는 의미하는 것입니다.

히스토그램(Histogram)에서 ‘그램(Gram)’은 그리스어에서 의미ㆍ정보를 뜻하는 ‘그라마(Gramma)’에서 유래한 것입니다.

출처: https://www.investopedia.com/

5. 히스토그램 필요성

히스토그램은 데이터 세트를 이해하고 분석하는 데 유용한 도구이며 데이터 분포를 시각화하는 데에 간단하고 효과적입니다.

• 데이터 시각화: 히스토그램은 데이터 세트 분포의 시각적 표현을 제공하여 패턴, 비대칭도 및 이상값을 신속하게 파악할 수 있습니다.
• 데이터 분석: 히스토그램은 데이터 세트의 모양과 분포를 이해하는 데 도움 됩니다. 히스토그램을 사용하여 데이터 세트의 평균, 중앙값 및 중심 추세를 결정하고 비대칭도 및 이상값을 식별할 수 있습니다.
• 데이터 세트 비교: 히스토그램을 사용하여 두 개 이상의 데이터 세트를 비교하여 유사점 혹은 차이점을 쉽게 확인할 수 있습니다.
• 데이터 압축: 히스토그램을 사용하여 값을 구간 계급으로 그룹화하여 데이터 세트의 크기를 줄일 수 있습니다. 데이터 저장하고 계산하는 데 제한된 프로그램에서 유용할 수 있습니다.
• 이상값 감지: 히스토그램을 사용하여 나머지 데이터와 크게 다른 이상값 또는 특이점을 식별하기 용이합니다. 이를 통해 통계 모델의 정확도를 높이고 데이터 수집 오류를 식별하는 데 사용할 수 있습니다.

6. 히스토그램 구성요소

히스토그램은 기본적으로 아래와 같은 요소로 구성됩니다.

• 구간(Bin): 빈도를 파악하기 위해 데이터를 균일하게 구간으로 나눕니다.
• 가로축(X축): 히스토그램에서 데이터가 분할된 구간을 나타냅니다.
• 세로축(Y축): 히스토그램에서 데이터값이 특정 구간에 속한 빈도수를 나타냅니다.
• 막대: 각 구간을 나타내는 막대이며, 막대 높이는 해당 구간에 속한 데이터 빈도수를 나타냅니다.

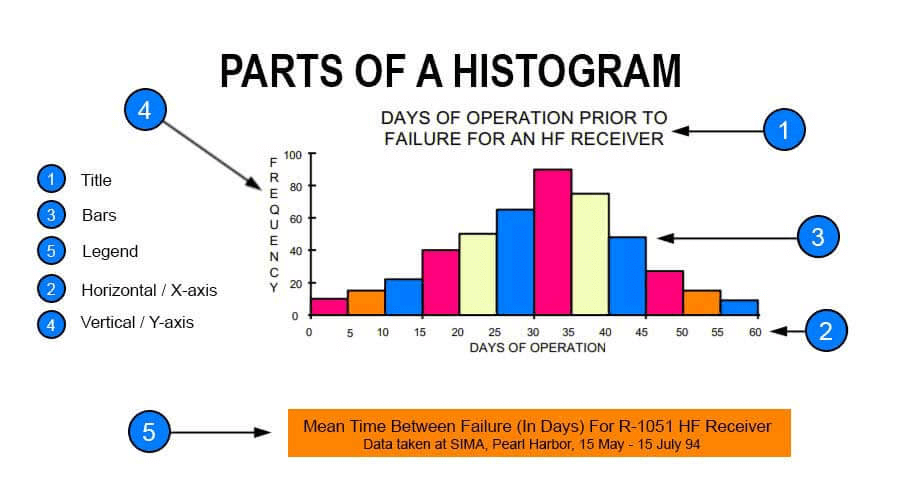
출처: https://www.wallstreetmojo.com/

Part 2: 히스토그램과 막대그래프의 차이점

히스토그램과 막대그래프는 모두 막대를 사용하여 데이터를 표시한다는 점에서 유사하지만, 다른 유형의 그래프입니다.

• 목적: 히스토그램의 목적은 연속 데이터 세트의 분포를 표시합니다. 반면에 막대그래프의 목적은 서로 다른 범주 또는 데이터 그룹 간의 비교를 표시하는 데에 있기 때문에 의도에 따라 막대로 표현하려는 범주 순서는 바뀔 수 있습니다.
• 구간: 히스토그램은 데이터 범위를 구간(Bin)이라고 하는 간격으로 균일하게 나누고 각 구간에 속하는 데이터 포인트의 수를 세어 생성됩니다. 각 막대의 높이는 각 그룹의 빈도수를 나타냅니다. 반면에 막대그래프는 연속 데이터뿐만 아니라 모든 유형의 데이터를 사용하여 만들 수 있으며 각 막대의 높이는 표시되는 데이터의 값을 나타냅니다.
• 막대 사이의 간격: 히스토그램에서 막대는 일반적으로 데이터가 연속적임을 나타내기 위해 막대 사이에 간격 없이 서로 인접하게 그려집니다. 막대그래프에서는 서로 다른 데이터 범주를 구분하기 위해 막대 사이에 간격을 두는 경우가 많습니다.

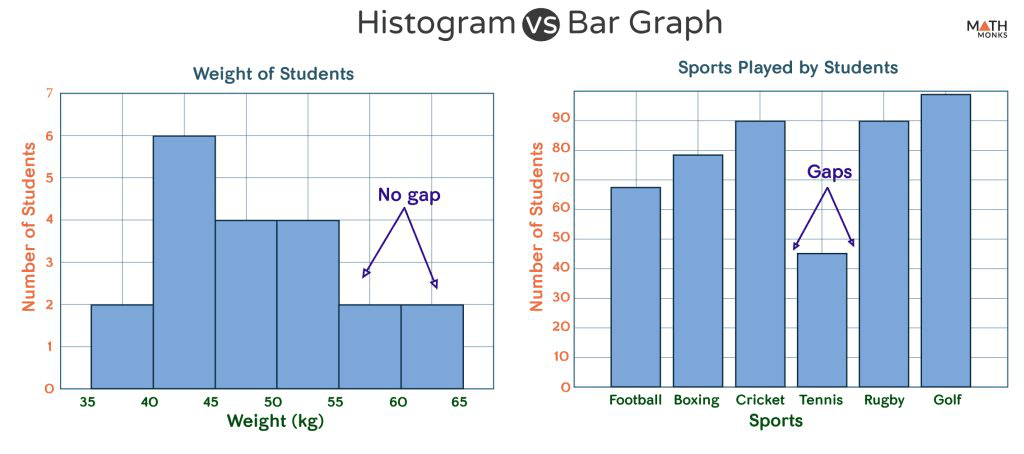
출처: https://mathmonks.com/histogram/

마무리

이렇게 히스토그램에 관한 모든 것을 알아보았습니다. 히스토그램은 방대한 데이터를 요약하여 시각화하는 데에 탁월하고 간단한 방법입니다. 데이터 시각화 작업은 업무하는 데에 필수적이기 때문에 히스토그램뿐만 아니라 여러 그래프를 익히고 활용하는 방법을 익혀야 일잘러로 거듭날 수 있습니다.

무료 이용