Los diagramas de Venn y diagramas de Euler son dos herramientas gráficas poderosas usadas ampliamente en el ámbito académico, comercial y tecnológico. Aunque ambos se utilizan para visualizar las relaciones entre diferentes conjuntos o categorías, existen diferencias significativas en sus estructuras y aplicaciones. En este artículo, vamos a descubrir estas diferencias, proporcionando ejemplos claros elaborados con Boardmix, una herramienta poderosa para la creación de diagramas.
¿Qué es un diagrama de Venn?
Un diagrama de Venn es una representación gráfica que muestra todas las posibles relaciones lógicas entre un número finito de conjuntos. Se compone de círculos superpuestos, cada uno representando un conjunto específico.
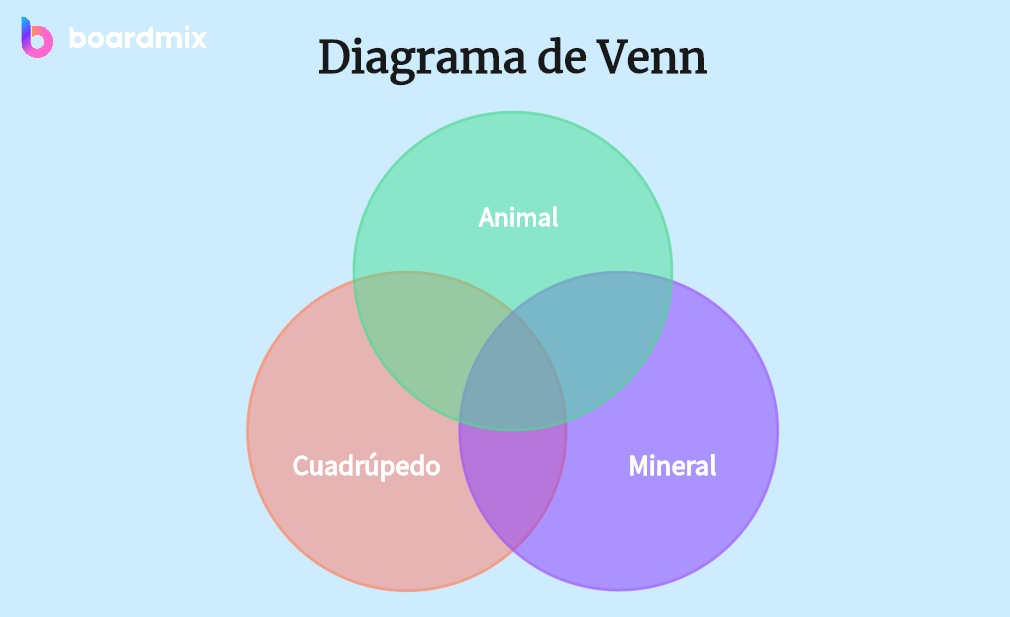
Crear diagrama de Venn en Boardmix
Historia y origen
El diagrama de Venn fue concebido en 1880 por John Venn, un matemático y filósofo inglés. Este tipo de diagrama se utiliza para representar gráficamente las relaciones entre distintos conjuntos de elementos, y es una herramienta fundamental en la teoría de conjuntos, una rama de las matemáticas.
La idea de los diagramas de Venn surgió en el contexto del desarrollo de la lógica simbólica durante el siglo XIX. George Boole, otro matemático británico, había creado lo que ahora conocemos como álgebra booleana, un sistema matemático que permite describir operaciones lógicas. Sin embargo, este sistema carecía de una representación visual eficaz.
Fue entonces cuando John Venn, inspirado por el trabajo de Boole, desarrolló los diagramas que llevan su nombre. Los diagramas de Venn son círculos que se superponen para mostrar todas las posibles relaciones lógicas entre los conjuntos representados.
Componentes y estructura
Un diagrama de Venn está compuesto por varias partes clave que trabajan juntas para ilustrar las relaciones entre diferentes conjuntos. Aquí están los componentes y la estructura de un diagrama de Venn:
- Círculos: Cada círculo en un diagrama de Venn representa un conjunto. El tamaño del círculo no tiene importancia en el diagrama, lo importante es cómo se relacionan los círculos entre sí.
- Superposición de círculos: Cuando dos o más círculos se superponen, esto representa la intersección de los conjuntos, es decir, los elementos que pertenecen a todos los conjuntos que se están superponiendo.
- Áreas no superpuestas: Las áreas de los círculos que no se superponen representan los elementos que son únicos para su conjunto respectivo.
- El espacio exterior al círculo: Todo el espacio fuera de los círculos en un diagrama de Venn representa el complemento del conjunto, es decir, todos los elementos que no están en el conjunto.
- Etiquetas: Los diagramas de Venn generalmente incluyen etiquetas para identificar qué representa cada círculo y qué representan las áreas superpuestas y no superpuestas.
En resumen, un diagrama de Venn utiliza la superposición y la separación de círculos para mostrar visualmente cómo se interrelacionan diferentes conjuntos. Es una herramienta poderosa para entender las relaciones lógicas y puede ser muy útil en una variedad de campos, desde las matemáticas hasta la ciencia de datos y la estadística.
Usos comunes
Los diagramas de Venn son una herramienta versátil y se utilizan en una variedad de campos para visualizar las relaciones entre conjuntos de elementos:
Matemáticas: En la teoría de conjuntos, los diagramas de Venn se utilizan para mostrar las relaciones entre diferentes conjuntos. Por ejemplo, pueden ilustrar la intersección, unión y diferencia entre los conjuntos.
Estadística: Los diagramas de Venn son útiles para visualizar las relaciones entre diferentes grupos de datos. Por ejemplo, pueden mostrar las intersecciones entre diferentes categorías de datos.
Lógica: En lógica, los diagramas de Venn se utilizan para demostrar las conclusiones lógicas a partir de un conjunto de premisas.
Informática: En informática y ciencia de datos, los diagramas de Venn pueden ayudar a visualizar las relaciones entre diferentes conjuntos de datos.
Educación: Los diagramas de Venn son una herramienta útil para enseñar a los estudiantes sobre las relaciones entre diferentes grupos o categorías.
Planificación y toma de decisiones: Los diagramas de Venn pueden ser útiles para visualizar las opciones y tomar decisiones informadas, por ejemplo, al comparar las características de diferentes productos o servicios.
Marketing y negocios: En marketing y negocios, los diagramas de Venn se pueden utilizar para comparar y contrastar ideas, estrategias o segmentos del mercado.
En resumen, los diagramas de Venn son una herramienta poderosa que puede ser utilizada en una amplia gama de disciplinas y contextos para ilustrar visualmente las interrelaciones entre diferentes conjuntos.
¿Qué es un diagrama de Euler?
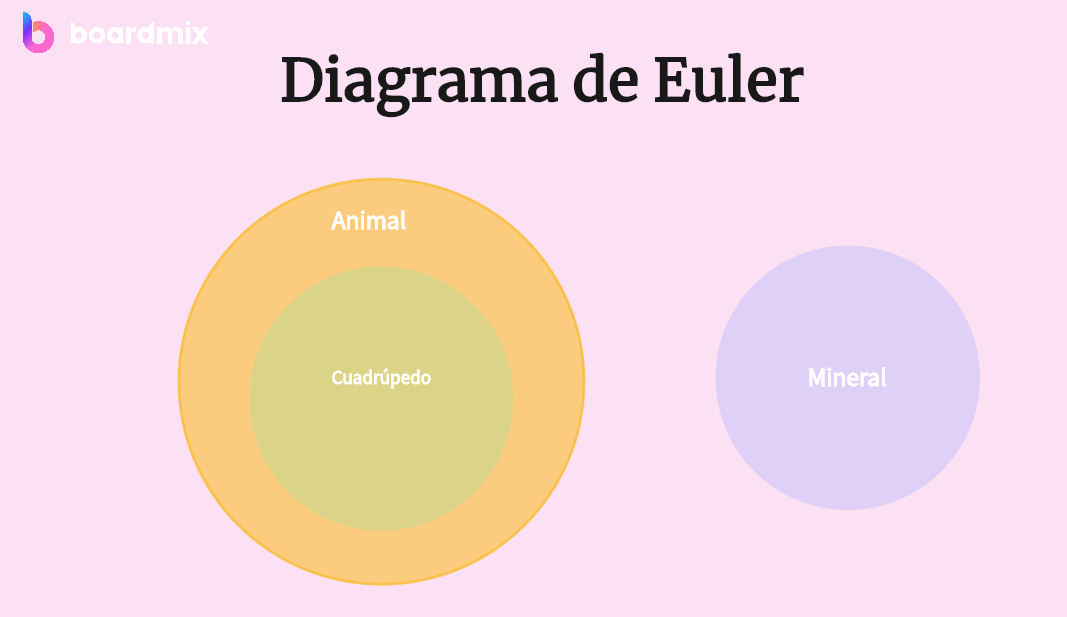
Crear diagrama de Euler en Boardmix
Un diagrama de Euler es una herramienta gráfica que se utiliza en matemáticas y lógica para representar conjuntos y sus relaciones. Los diagramas de Euler normalmente consisten de simples curvas cerradas en el plano que son usadas para describir conjuntos. Las relaciones espaciales entre las curvas (superposición, contención o ninguno) corresponden, respectivamente, a relaciones de intersección, subconjunto y disjuntes, de la teoría de conjuntos.
Estos diagramas son una generalización del bien conocido diagrama de Venn, el cual representa todas las posibles intersecciones entre los conjuntos presentes dados.
Historia y origen
El Diagrama de Euler lleva el nombre de Leonhard Euler, un matemático suizo del siglo XVIII que hizo contribuciones significativas en varias áreas de las matemáticas. Aunque los conceptos que representan estos diagramas han existido durante mucho tiempo, se atribuye a Euler la introducción de este método específico de visualización.
Euler inicialmente introdujo estos diagramas como una forma de representar syllogisms, que son formas de razonamiento deductivo en la lógica. Los diagramas de Euler se utilizaban para ilustrar las relaciones lógicas entre diferentes conjuntos o conceptos, lo que facilitaba el proceso de razonamiento y resolución de problemas.
Desde su introducción por Euler, estos diagramas han sido ampliamente adoptados y adaptados en diversas disciplinas, desde las matemáticas hasta la informática y la teoría de conjuntos. Han demostrado ser una herramienta valiosa para visualizar y entender las relaciones complejas entre diferentes conjuntos o grupos.
Componentes y estructura
Un diagrama de Euler se compone principalmente de los siguientes elementos:
- Conjuntos: Se representan mediante círculos o elipses en el diagrama. Cada círculo representa un conjunto distinto.
- Elementos: Los elementos de un conjunto se representan dentro del círculo correspondiente. Si un elemento pertenece a más de un conjunto, se coloca en la zona de intersección de los círculos correspondientes.
- Relaciones: Las relaciones entre los conjuntos se representan mediante la posición relativa de los círculos. La intersección de dos círculos representa la intersección de dos conjuntos (los elementos que tienen en común). Si un círculo está completamente dentro de otro, indica que un conjunto es subconjunto del otro.
- Área fuera de los círculos: Todo lo que está fuera de los círculos representa el complemento universal, es decir, todos los elementos que no pertenecen a ninguno de los conjuntos representados.
La estructura del diagrama de Euler depende del número y las relaciones entre los conjuntos que se estén representando. Puede ser tan simple como dos círculos que se superponen parcialmente para representar dos conjuntos con algunos elementos en común, o puede ser más complejo con múltiples círculos superpuestos para representar múltiples conjuntos y sus interrelaciones.
Usos comunes
Los diagramas de Euler tienen una amplia variedad de usos en diferentes campos debido a su capacidad para representar visualmente las relaciones entre conjuntos:
Matemáticas: En matemáticas, los diagramas de Euler se utilizan para ilustrar las relaciones entre conjuntos y subconjuntos. Esto puede ser especialmente útil en la enseñanza de conceptos como la unión, intersección y diferencia de conjuntos.
Lógica: Los diagramas de Euler son una herramienta valiosa en lógica para visualizar y entender syllogisms, que son formas de razonamiento deductivo.
Informática: En informática, los diagramas de Euler pueden ser utilizados para representar estructuras de datos, especialmente en la visualización de relaciones complejas entre diferentes conjuntos de datos.
Estadística: En estadística, estos diagramas pueden ayudar a visualizar las relaciones entre diferentes grupos en un conjunto de datos, facilitando el análisis y la interpretación.
Gestión de proyectos: Algunos gestores de proyectos utilizan diagramas de Euler para visualizar las relaciones entre diferentes grupos o equipos en un proyecto, lo que puede ayudar a identificar posibles problemas o áreas de colaboración.
Marketing: En marketing, los diagramas de Euler pueden ser utilizados para segmentar audiencias y entender las intersecciones entre diferentes grupos demográficos o comportamentales.
En resumen, los diagramas de Euler son una herramienta versátil que puede ser útil en cualquier campo que requiera la visualización y comprensión de las relaciones entre conjuntos.
Comparación detallada entre el diagrama de Venn y el diagrama de Euler
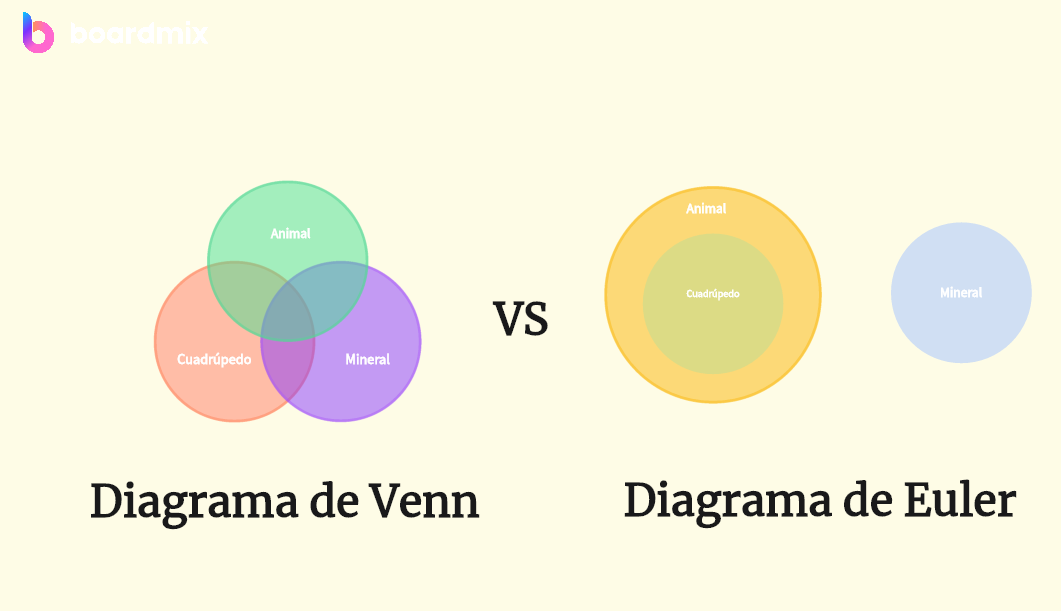
Los diagramas de Venn y Euler son herramientas visuales que comparten el propósito fundamental de representar conjuntos y relaciones, pero difieren en su enfoque y estructura. A continuación, exploraremos las similitudes y diferencias clave entre estos dos tipos de diagramas, destacando sus características distintivas.
Similitudes:
Representación de conjuntos
Tanto el diagrama de Venn como el de Euler se utilizan para visualizar la relación entre conjuntos. Ambos ofrecen una representación gráfica intuitiva de la intersección y la diferencia entre conjuntos, facilitando la comprensión de relaciones complejas.
Utilización en lógica y teoría de conjuntos
Ambos tipos de diagramas tienen aplicaciones significativas en lógica y teoría de conjuntos. Se utilizan para ilustrar conceptos como la intersección, unión y diferencia entre conjuntos, lo que los hace valiosos en disciplinas que dependen de la representación gráfica de relaciones lógicas.
Flexibilidad en la representación
Tanto el diagrama de Venn como el de Euler permiten la representación de conjuntos superpuestos, aunque lo hacen de manera diferente. La flexibilidad en la representación es esencial para abordar una variedad de situaciones y conjuntos complejos.
Diferencias:
Estructura visual
La diferencia visual más evidente radica en la estructura de los diagramas. Mientras que el diagrama de Venn utiliza círculos superpuestos para representar conjuntos y sus intersecciones, el diagrama de Euler utiliza regiones cerradas para representar conjuntos y subconjuntos, evitando la superposición.
Superposición de conjuntos
En el diagrama de Venn, la superposición de círculos indica la existencia de elementos comunes entre conjuntos. En cambio, el diagrama de Euler evita la superposición, representando cada conjunto como una región independiente. Esto puede hacer que el diagrama de Euler sea más adecuado para conjuntos que no tienen intersección.
Número de conjuntos representados
El diagrama de Venn es más versátil cuando se trata de representar conjuntos múltiples. Puede manejar conjuntos que se intersecan en varias combinaciones. Por otro lado, el diagrama de Euler es más efectivo cuando se trata de conjuntos que no se superponen o que tienen intersecciones más simples.
Historia y desarrollo
Los diagramas de Venn fueron desarrollados por John Venn a fines del siglo XIX, mientras que los diagramas de Euler fueron conceptualizados por Leonhard Euler en el siglo XVIII. La diferencia temporal entre estos dos desarrollos históricos también ha influido en sus enfoques y aplicaciones.
¿Cuándo utilizar un diagrama de Venn o un diagrama de Euler?
Es esencial comprender que ambos diagramas son herramientas visuales poderosas para representar relaciones y conjuntos. Sin embargo, su aplicación puede variar dependiendo de la situación.
El diagrama de Venn es una elección perfecta cuando se necesita ilustrar la intersección y la relación entre diferentes conjuntos. Estos diagramas son especialmente útiles cuando se trata de comparar y contrastar grupos de datos. Por ejemplo, si está comparando las características de diferentes modelos de coches, un diagrama de Venn podría ser una forma efectiva de visualizar las similitudes y diferencias.
Por otro lado, el diagrama de Euler se utiliza mejor cuando se quiere representar conjuntos que están completamente contenidos dentro de otros. Este tipo de diagramas es ideal para representar jerarquías o subconjuntos. Imagine que está organizando una empresa y quieres visualizar la estructura organizativa; en este caso, un diagrama de Euler sería la opción más adecuada.
En resumen, tanto los diagramas de Venn como los de Euler son herramientas valiosas en el análisis y presentación de datos. La elección entre uno u otro dependerá del tipo específico de datos que esté manejando y del mensaje que quiera transmitir. Recuerde siempre considerar el contexto y el objetivo al seleccionar la herramienta más adecuada.
Maximizando el potencial de los diagramas de Venn y Euler con Boardmix
Los diagramas de Venn y Euler son herramientas poderosas para representar relaciones y conjuntos, y Boardmix emerge como una plataforma eficiente para su creación. Maximizar el potencial de estos diagramas implica no solo comprender sus características distintivas, sino también aprovechar al máximo las funcionalidades de Boardmix.
Boardmix es una plataforma revolucionaria que se especializa en la visualización de datos. Con su interfaz intuitiva y sus múltiples funciones, Boardmix puede transformar los simples diagramas de Venn y Euler en visualizaciones dinámicas e interactivas. Imagine poder ver en tiempo real cómo se superponen sus conjuntos de datos, o poder ajustarlos a medida que cambian sus necesidades.
Funciones claves de Boardmix:
- Facilidad de uso: Boardmix presenta una interfaz de usuario intuitiva que es fácil de aprender y utilizar. Esto permite a los usuarios, independientemente de su nivel de experiencia técnica, crear y editar diagramas con facilidad.
- Personalización avanzada: Con Boardmix, los usuarios tienen un control total sobre la personalización de sus diagramas. Pueden cambiar el tamaño, color, forma, ubicación y orientación de cada conjunto en los Diagramas de Venn y Euler, lo que les permite adaptar los diagramas a sus necesidades específicas.
- Herramientas versátiles para dibujar: Boardmix ofrece una gama completa de herramientas para dibujar y ajustar conjuntos. Esto incluye formas predeterminadas para conjuntos en diagramas de Venn y Euler, así como herramientas de dibujo libre para representaciones más creativas o únicas.
- Funcionalidad drag-and-drop: Boardmix también integra funcionalidad drag-and-drop (arrastrar y soltar), permitiendo a los usuarios mover y organizar conjuntos con facilidad. Esta función simplifica enormemente el proceso de diseño del diagrama.
- Compartir y colaborar: Boardmix también facilita el trabajo colaborativo. Los usuarios pueden compartir sus diagramas con otros fácilmente, permitiendo la colaboración en tiempo real. Esta funcionalidad es especialmente útil para equipos que necesitan trabajar juntos en la creación y análisis de diagramas.
- Exportar en diferentes formatos: Los usuarios pueden exportar sus diagramas en una variedad de formatos, incluyendo JPEG, PNG, PDF, SVG entre otros. Esta flexibilidad hace que sea fácil para los usuarios presentar y compartir sus diagramas en una variedad de contextos.
Conclusión
Los diagramas de Venn y Euler son poderosas herramientas visuales para la representación de conjuntos y sus interrelaciones. Mientras que los diagramas de Venn son más exhaustivos, pueden volverse complicados y confusos con un gran número de conjuntos. Los diagramas de Euler, por otro lado, son más simples y claros, pero no muestran todas las posibles interrelaciones. Al final, la elección depende del propósito y del tipo de información que se quiera visualizar. Y no olvide utilizar la herramienta online de pizarra Boardmix para profundizar en estos dos diagramas. ¡Pruébelo ahora!